作者:沈宜儒 / 臺灣大學計算機及資訊網路中心程式設計組資訊工程師
您曾在程式碼看過不明所以的常數像是0xFFD700或是86400嗎?是否疑惑過這個常數的用途,是怎麼定義的?這些都可以算是程式中的魔術數字,本文會介紹甚麼是魔法數字,說明它是否是寫程式的好習慣,並介紹一些魔術數字的例子。
甚麼是程式設計中的魔術數字
程式設計中,如果沒有解釋就出現了一個不知道意涵的數值,那麼那個數值就可以稱為魔術數字(magic number)。因為沒有解釋,所以容易讓人不清楚數值的意義。如果該數字在程式中反覆出現,在數值需要修改時也會有需要逐一修改的問題。以下為一些魔術數字的案例:
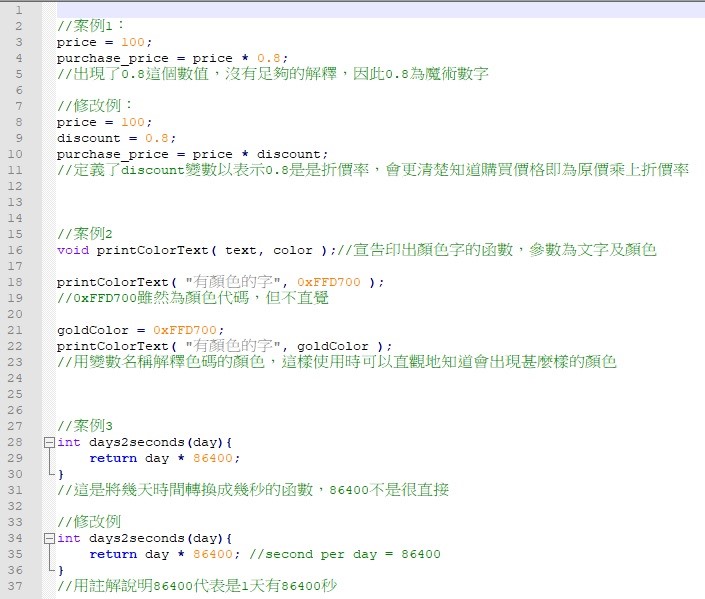
圖1:一些魔術數字的案例
在案例1,第4行程式碼出現了0.8,但缺乏了0.8是甚麼的資訊。如果先定義好變數discount表示折價率為0.8,我們在使用時就知道購買價格(purchase_price)即為價格乘上折價率,若程式後面有再使用折價率的話,就可以直接用discount,而不是反覆使用常數0.8。修改後,若折價率需要常修改的話,就只要修改discount的數值,不用逐行檢查那些常數需要修改。
在案例2,雖然我們可以直接用色碼指定印出文字的顏色,但如果先用有顏色名稱的變數代表色碼,使用顏色變數會讓程式碼可讀性更好。
在案例3,有些人會不清楚86400代表甚麼,這樣86400就可能是魔術數字,透過增加註解,表示86400的由來是1天有86400秒,這樣程式就更容易了解。
難以理解的魔術數字─0x5f3759df
在西元2000年初,網路上在討論一款遊戲─《雷神之鎚III》中的程式碼,程式中實作了求反平方根的快速演算法(圖2),其中的10行突然出現了16進未表示的常數─0x5f3759df,並註解了「這是怎麼回事?」。

圖2:《雷神之鎚III》程式碼中的反平方根快速演算法,速度比直接使用除法快4倍
要理解這段程式碼,需要對電腦儲存數字的方法有所概念,從圖2第9行到的11行,程式將浮點數y當作整數i來運算,並用常數0x5f3759df減去i/2,以結果轉回浮點數。第12行為牛頓法來提高精確度。
至於為什麼這樣運算可以求出反平方根的近似值,0x5f3759df又是怎麼決定的,這又是數學問題了。詳細的推導跟計算可以參考文末的參考資料。
結論
考慮到程式的可讀性還有維護、擴充的需求,編寫程式時應該避免缺少說明而產生的魔術數字。而透過註解,定義常數名稱來化解魔術數字。至於文末的魔術數字0x5f3759df,雖然可以定義變數名稱R表示,但這也無法解釋其原理,而要在程式碼中解釋原理則有相當難度。
參考資料
- 魔術數字(程式設計) – 維基百科:
https://zh.wikipedia.org/wiki/%E9%AD%94%E8%A1%93%E6%95%B8%E5%AD%97_(%E7%A8%8B%E5%BC%8F%E8%A8%AD%E8%A8%88)
- 反平方根快速演算法 – 維基百科:
https://zh.wikipedia.org/wiki/%E5%B9%B3%E6%96%B9%E6%A0%B9%E5%80%92%E6%95%B0%E9%80%9F%E7%AE%97%E6%B3%95
- Origin of Quake3's Fast InvSqrt():
https://www.beyond3d.com/content/articles/8/
- 0X5F3759DF: Quake III Arena, IEEE 754, and the Importance of Commenting Code:
https://www.ismailzai.com/blog/0x5f3759df/