作者:郭偉森 / 臺灣大學計算機與資訊網路中心作業管理組工讀生
隨著計算機的運算速度增加,資訊人才的培養常態化,現在走在任何大學校園,是個同學就會有七到八個人都會寫程式。雖然如此,但是很多人對於程式究竟可以拿來幹嘛的都沒有一定的了解,甚至還有些人對於程式的概念就停留在經典的課堂作業,「印星星」。其實,寫程式可以做的事情非常的廣,從大家熟悉的機器學習,到硬體的控制,和一些資料的收集,處處都可以使用程式來為我們代勞,而在這篇文章就是要使用Python作為程式語言編寫最佳化演算法,分享一些心得。
什麼是基因最佳化演算法?
所謂最佳化俗話來說就是用最低的成本來達到最高的效率。這和大家所學過的數學函數一樣,設一f(x)等於x的二次方的時候一定會有一個輸入可以取得最小值,在這個例子裡,當x輸入等於0的時候,這個函式將會得到0這個結果,其他的值在輸入之後都會得到比0還要大的結果,這個就是最佳化的簡單概念。然而這個世界的運行是複雜的,倘若我們所輸入的參數不只有一個的時候,且所有可變參數都非簡單次方,這就非常的難以找到最佳解。這就是為什麼我們需要最佳化演算法,最佳化演算法的出現幫我們解決了這個問題。
在這篇文章中要使用的演算法就是目前最常用的最佳化演算法之一,基因演算法。這套演算法算是一種仿生的演算法,利用了生物適者生存,劣者淘汰的特性來進行編寫的演算法。雖然聽起來有點政治不正確,但是這套演算法很有效的解決很多需要快速收斂的難題。下面是這套演算法的流程:

圖一:基因演算法流程[1]。
從圖一可見,基因演算法會產生一個初始的「人口(population)」,這個所謂的人口是由亂數產生一堆0和1,使其成為一段長長的二進制的數字,人口就是由很多的二進制數字組成的。接下來就需要計算所謂的fitness value,這個fitness value的定義就是由編寫程式的人自己決定,在這個部分我個人會喜歡以「0」作為一個參考值。這是因為通常會拿來進行最佳化演算法的問題都會是尋找極大值或極小值,我們可以這幾組基因的解計算它的解是否靠近「0」來判斷其為最大或最小。
計算這個fitness的邏輯如下,fitness會依據每個題目要求的最佳解的不同,會有不一樣的定義。但是其概念是相通的。已知待解決的問題擁有最高或最低值,所以可以直接使用歸一化的方式計算fitness。其公式如下:
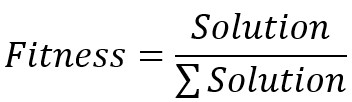
考慮到現實中會因為不知道待解決問題的最低或最高值,fitness是無法直接使用上面的方式計算。不過這個可以透過同時考慮最高值和最低值,並直接比較其的解,通過使用if… else…來去除壞值。Fitness可以透過上面的公式計算,且逼近最佳解。透過定義fitness,我們可以利用它來覺得進行產生下一代會用到的染色體,也就是說,fitness越大,染色體被選中進行繁衍的幾率越大。
在這之後,fitness value會告訴程式關於這段基因的優劣性,也就是根據fitness value的大小判斷其是否需要進行保留(Selection)或基因變化。基因變化也稱為基因演算法參數,就是圖一所顯示的Crossover、Mutation和Reproduction。在下一段落將會更詳細的介紹這三個參數的內容。
基因演算法參數
先說說Crossover,顧名思義就是交換。選擇兩組fitness較好的基因然後選擇隨機的節點進行切割並互相交換。網路上也有很多人會選擇多節點的切割,可以依據待解決問題的複雜度做調整,一般上較普通的問題選擇一個節點即可。示意圖如下:
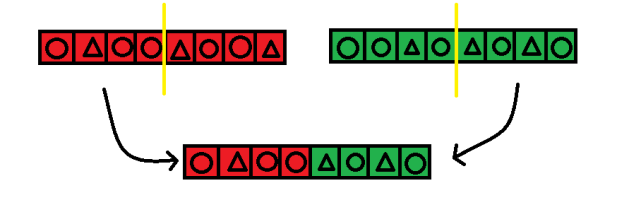
圖二:Crossover示意圖。
如圖所示,經過運算,將只會產生一條染色體。有時候會因為過早收斂的問題,通常發生這個Crossover演算法的機率都不會超過50%,這樣可以減少因為進入某個非極值的臨界點而無法跳出的問題,也就是過早收斂。
Mutation,變異,顧名思義就是將其中一個染色體的基因更改成另外一個。在編寫過程中會完全隨機選擇一組基因的其中一個染色體來進行變異,例如把原本的「0」變成「1」。這樣就為基因演算法提供了一些不確定性,避免演算過程中計算機判斷該計算已經收斂。
Reproduction相對於其他兩個運算子相對簡單。直接選擇fitness較好的基因然後複製傳到下一代。但是如果複製的幾率太高,也會有過早收斂的情況,所以通常只會有15%的機會使用這個參數。
這三個參數的選用個人是喜歡透過「機率」的方式來進行,在網路上也有很多演算法大師會使用三者並行的方式。「機率」的好處就是可以增加演算過程中的不確定性,這樣就可以更符合最佳化的目的。另外,倘若題目會出現過早收斂的情況,也可以透過更改每一個參數的發生機率來避免。
演算結束判斷
演算結果判斷是一個很玄的東西。很多人會以多次演算的結果是否為同一結果為判斷,例如當演算結果達到某個最佳解超過n次之後就停止演算。然而,這個方法的缺點就是演算結果有可能收斂在某個非最佳解。所以在有些已知最佳解的情況下,個人偏好使用以次數作為判斷,也就是直接演算n次,如果設備的效能允許,可以直接選擇1000次或以上。雖說如此,但是這個演算結束的判斷會因為演算法效率低而導致在演算結束時還沒有得到最佳解,也就是過晚收斂。這個判斷方式比較適合設備效能高和不追求程式執行速度的情況下使用,像是一些汽車工業的最佳解演算,例如煞車就需要很高效率的演算法,前者的判斷更符合要求。
使用Python執行結果
說了那麼多,是時候使用Python執行上面所提到的演算法了。此次要解決的問題是經典的數學式子,Shubert Function,其數學式子如下:
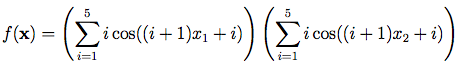
光看式子,很難理解為什麼需要找到這個問題的最佳解,看了其可視化曲面就會知道為什麼需要透過最佳化演算法解決。
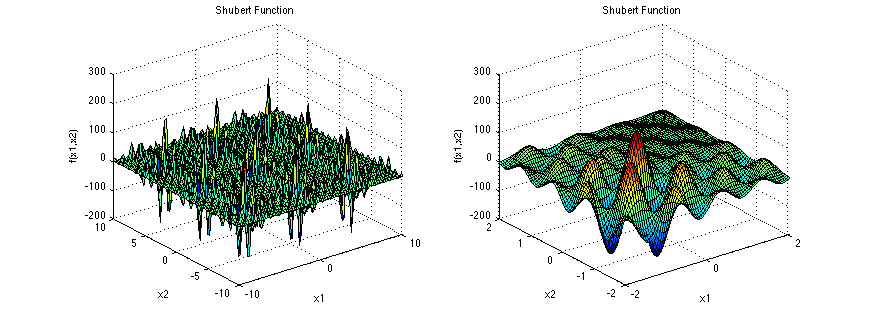
圖三:Shubert Function可視化[2]。
從圖三可以知道這個數學式子有很多的臨界點,其中只有一個最佳解,在編寫最佳化演算法的時候這一方程式很適合用來當成模板來使用。再說說這個式子的最佳解,當x1和x2的輸入介於-10到10之間(含)之後,其最佳解值為 -186.7309。
說了那麼多,開始執行,下圖是使用python執行演算法的結果,另外會紀錄每一筆演算結果的紀錄,並展示其「收斂」的趨勢:
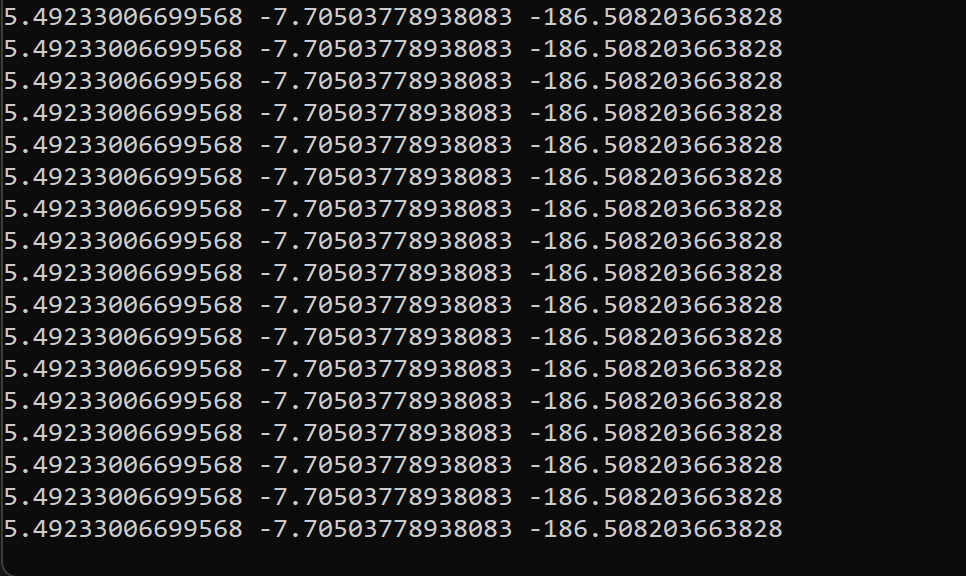
圖四:使用Python進行基因演算法計算Shubert Function結果。
以下是收斂趨勢:
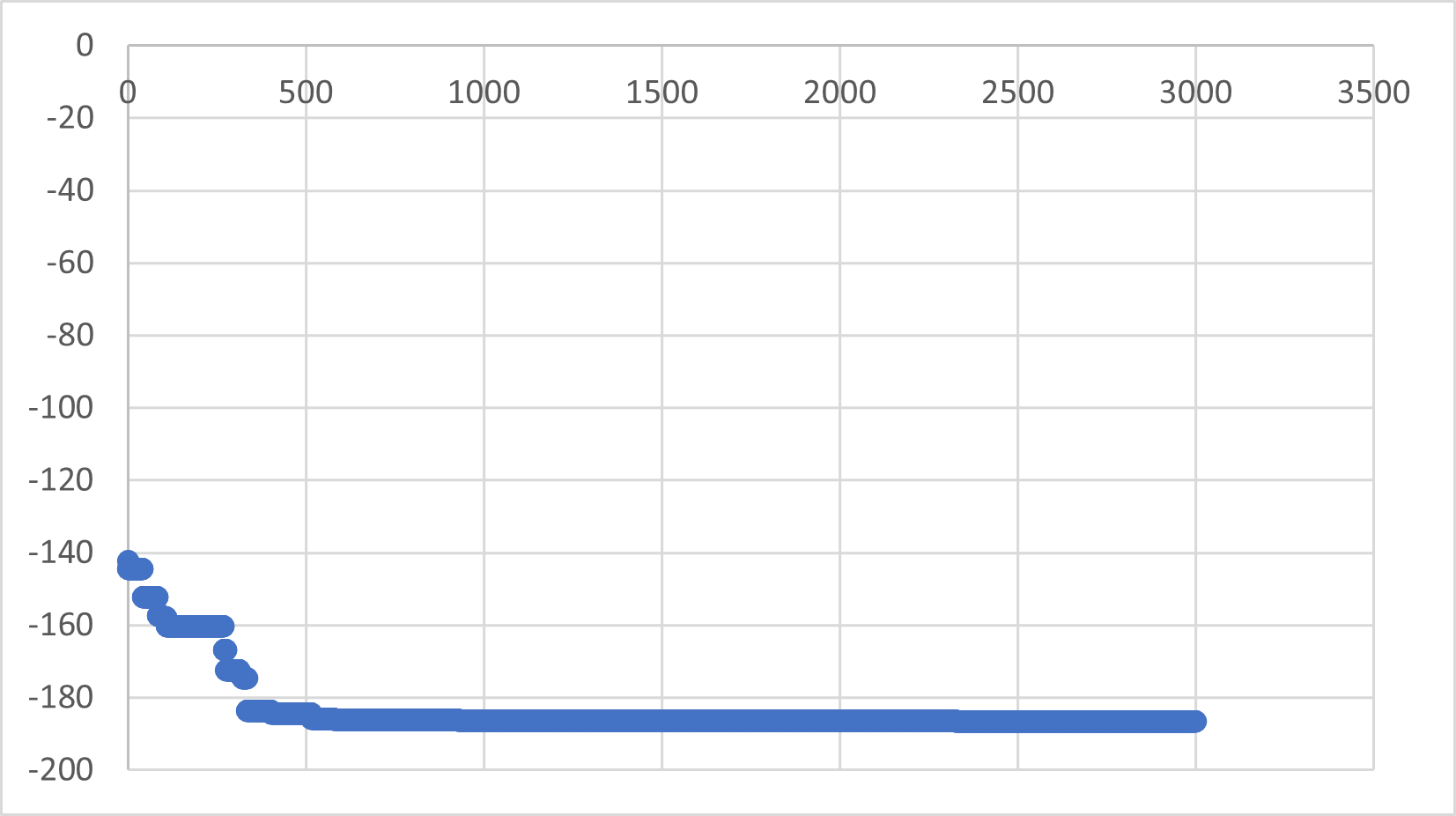
圖五:演算法收斂趨勢。
從圖四可以看到,在執行3000次的演算之後,可以得到-186.50的最佳解,其誤差差不多為0.12%,x1和x2的值為5.49和-7.71。除了這兩個解之外,可以透過再執行程式得到不一樣的解,只要輸出值接近-186.73即是最佳解。
另外,可以從圖五觀察,在差不多執行500次演算法了之後,演算就進入了收斂的情況。這代表演算法的效率極高。同樣流程的程式,使用Python下來其執行效率更高。之前在使用C#來執行同樣的演算法,需要執行快1000-1500次才能夠收斂。因此使用Python作為這套演算法的編寫語言是非常理想的。
結語
綜上所述,在科技日新月異的時代,程式可以為我們解決很多很多的問題,絕對不是如開頭所說的「印星星」而已。另外,因為Python的語法相對其他程式語言來得簡單,因此大大的降低編寫程式的門檻。在這個講求效率的時代,每個人都可以為自己編寫一套用來「解決問題」的程式,就從現在開始吧!
參考
[1]Albadr, Musatafa & Tiun, Sabrina & Ayob, Masri & Al-Dhief, Fahad. (2020). Genetic Algorithm Based on Natural Selection Theory for Optimization Problems. Symmetry. 12. 1-31. 10.3390/sym12111758.
[2]https://www.sfu.ca/~ssurjano/shubert.html